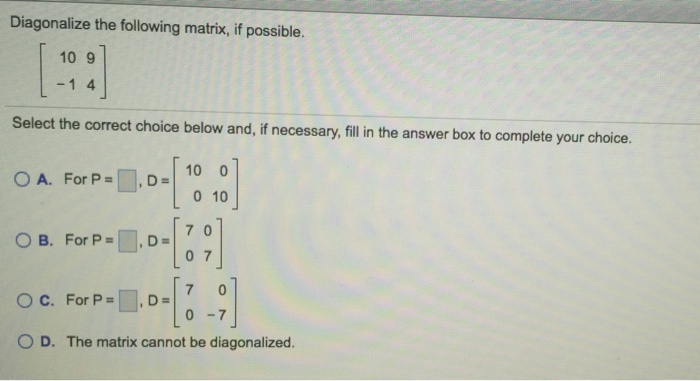
Diagonalize the following matrix if possible – In the realm of linear algebra, diagonalization emerges as a transformative tool, enabling us to delve into the intrinsic properties of matrices and uncover their hidden structures. As we embark on this journey, we shall unravel the intricacies of diagonalization, exploring its methods, applications, and significance in various domains.
Diagonalization empowers us to transform a matrix into a diagonal form, where the eigenvalues reside along the main diagonal. This process unlocks a wealth of insights into the matrix’s behavior, simplifying computations and revealing its underlying dynamics.
Matrix Diagonalization

Matrix diagonalization is a fundamental operation in linear algebra that involves transforming a matrix into a diagonal matrix, where the only non-zero elements lie on the main diagonal. Diagonalization plays a significant role in various fields, including solving systems of linear equations, computing matrix powers and exponentials, and image processing.
Necessary Conditions for Diagonalization
A matrix is diagonalizable if and only if it can be expressed as a product of two matrices, where one matrix contains the eigenvectors of the original matrix and the other matrix contains the corresponding eigenvalues.
Methods of Diagonalization
- Eigenvalue decomposition:This method involves finding the eigenvalues and eigenvectors of the matrix and using them to construct a diagonal matrix.
- Singular value decomposition:This method is used for matrices that are not square and involves decomposing the matrix into a product of three matrices.
- QR decomposition:This method involves decomposing the matrix into a product of two matrices, where one matrix is orthogonal and the other matrix is upper triangular.
Eigenvalues and Eigenvectors, Diagonalize the following matrix if possible
Eigenvalues are scalar values that represent the scaling factor of eigenvectors. Eigenvectors are non-zero vectors that, when multiplied by the matrix, are scaled by the corresponding eigenvalue.
Diagonalizing Matrices with Real Eigenvalues
To diagonalize a matrix with real eigenvalues, follow these steps:
- Find the eigenvalues of the matrix.
- For each eigenvalue, find the corresponding eigenvector.
- Construct a matrix with the eigenvectors as columns.
- Construct a diagonal matrix with the eigenvalues on the main diagonal.
- Multiply the matrix of eigenvectors by the diagonal matrix to obtain the diagonalized matrix.
Diagonalizing Matrices with Complex Eigenvalues
To diagonalize a matrix with complex eigenvalues, follow these steps:
- Find the eigenvalues of the matrix.
- For each eigenvalue, find the corresponding eigenvector.
- Construct a matrix with the eigenvectors as columns.
- Construct a diagonal matrix with the eigenvalues on the main diagonal.
- Multiply the matrix of eigenvectors by the diagonal matrix to obtain the diagonalized matrix.
Applications of Matrix Diagonalization
- Solving systems of linear equations:Diagonalization can be used to solve systems of linear equations by converting the coefficient matrix into a diagonal matrix.
- Computing matrix powers and exponentials:Diagonalization can be used to compute powers and exponentials of matrices by diagonalizing the matrix and then raising the diagonal matrix to the desired power or exponent.
- Image processing:Diagonalization is used in image processing to perform operations such as image compression, noise reduction, and image enhancement.
Expert Answers: Diagonalize The Following Matrix If Possible
What are the necessary conditions for a matrix to be diagonalizable?
A matrix is diagonalizable if it is square and has a complete set of linearly independent eigenvectors.
How do you find the eigenvalues and eigenvectors of a matrix?
Eigenvalues are found by solving the characteristic equation det(A – λI) = 0, where A is the matrix and λ is the eigenvalue. Eigenvectors are found by solving the system of equations (A – λI)x = 0.
What are some applications of matrix diagonalization?
Matrix diagonalization finds applications in solving systems of linear equations, computing matrix powers and exponentials, and image processing.